4. 오차역전파법(1)

※ 오차역전파법(backpropagation)

- 가중치 매개변수의 기울기를 효율적으로 계산하는 방법

 

1. 수식을 통한 설명

2. 계산 그래프를 통한 설명

 

※ 계산 그래프

- 자료구조 Graph를 이용하여 노드와 에지를 사용하여 표현

 

순전파 : 계산 그래프(왼쪽 -> 오른쪽)

역전파 : 계산 그래프(오른쪽 -> 왼쪽)

 

■ 국소적 계산

- 전체에서 벌어지는 일과 상관없이 자신과 관계된 정보만으로 결과 출력이 가능함.

- 중간 계산 결과를 모두 보관할 수 있음.

- 역전파를 통해 '미분'을 효율적으로 계산 할 수 있음.

 

<밑바닥부터 시작하는 딥러닝 1> 152p

 

공부를 하는 교재의 그림을 참고하여 설명을 해보겠다. 순전파를 통해서 100원짜리 사과 2개를 산 후 소비세 10%가 붙을 때 지출하는 금액을 나타낼 수 있었다. 이를 역전파를 통해서 살펴보면 1 -> 1.1 -> 2.2의 순서로 미분 값을 전달하게 된다. 사과가 1원 올랐을 때 최종 금액이 2.2원 오른다는 변화량을 나타낼 수 있고, 이를 통해 사과 가격에 대한 지불 금액의 미분값은 2.2 인 것을 확인해 볼 수 있다. 또한, 중간까지 구한 미분 결과를 공유할 수 있어서 다수의 미분 관리에도 효율적이다.

 

 

※ 연쇄법칙

- 합성 함수 미분에 대한 성질로 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타내는 법칙

 

 

위 식을 통해 연쇄법칙을 설명할 수 있는데, x에 대한 z의 미분을 (t에 대한 z의 미분) + (x에 대한 t의 미분) 꼴로 나타내어 준 것이다. 이를 계산 그래프로 나타내어 보면 조금 더 확실히 와 닿는다.

 

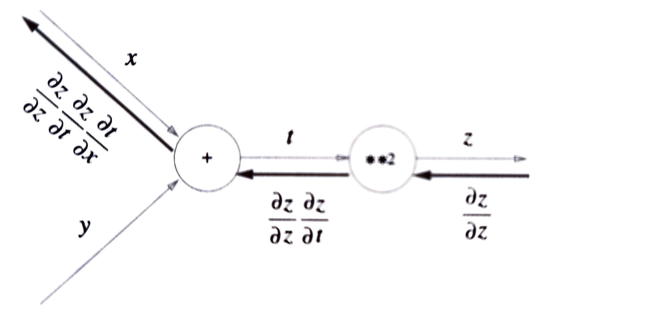
<밑바닥부터 시작하는 딥러닝> 154p

 

이 계산 그래프를 보면 역전파 방식이 연쇄법칙과 완전히 같은 구조를 이루고 있다는 것을 깨달을 수 있을 것이다. z에서 t로 갈 때 (t에 대한 z의 미분)을 곱해주고, 다시 t에서 x로 갈 때 (x에 대한 t의 미분)을 곱해준다. 이렇게 (x에 대한 z의 미분)을 역전파 방식으로 표현 할 수 있는 것이다.

 

개인적으로 참고할 만한 사이트 였고, 이를 통해 연쇄 법칙을 완벽히 이해할 수 있어서 링크를 첨부한다.

[벡터 미적분학] 연쇄 법칙(Chain rule) (tistory.com)

[벡터 미적분학] 연쇄 법칙(Chain rule)

 

 

※ 연쇄 법칙을 통한 역전파 계산

 

■ 덧셈 노드의 역전파

 

z = x + y 라는 식을 대상으로 역전파를 살펴 보자. x에 대한 z의 미분 = 1, y에 대한 z의 미분 = 1이다.

 

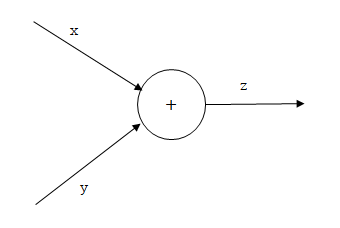
순전파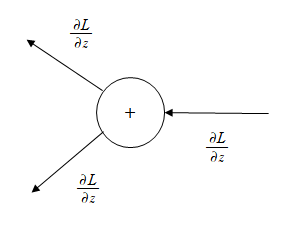

역전파

 

이렇게 순전파와 역전파를 비교해 보면 L이라는 Global Gradient에 대해 상류로 부터 전해진 z에 대한 L의 미분 값(Local Gradient)이 그대로 다음 노드로 전달되고 있는 것을 볼 수 있다.

 

 

■ 곱셈 노드의 역전파

 

z = x y 라는 식으로 곱셈 노드의 역전파를 살펴보자. x에 대한 z의 미분 = y, y에 대한 z의 미분 = x가 된다. 이를 통해 순전파와 역전파를 살펴보자.

 

순전파

 

역전파

 

덧셈 노드의 역전파와 비교했을 때, 한 가지 차이점을 발견할 수 있을 것이다. y와 x가 곱해진 것을 확인할 수 있다. 그런데 서로 위치가 바뀌어 z에 대한 L의 미분에 곱해진 것을 확인 가능하다.

 

 

이렇게 덧셈 노드와 곱셈 노드에서의 역전파 차이를 연쇄 법칙을 통해서 알아보았다. 덧셈의 역전파에서는 상류의 값을 그대로 흘려보내면서 순방향 입력 신호의 값은 필요하지 않았다. 하지만, 곱셈의 역전파는 순방향 입력 신호의 값을 서로 교차하여 곱해서 나타내므로 역전파 출력 신호를 알기 위해서는 순방향 입력 신호의 값이 필요하다. 그래서 곱셈 노드를 구현할 때는 반드시 순전파의 입력 신호를 변수에 저장해 둔다.

 

이제 위의 국소적 계산 그래프를 다시 한 번 살펴보자. 곱셈 노드의 역전파이므로 1.1 = 1 * 1.1(소비세 입력 값),

2.2 = 1.1 * 2(사과의 개수 입력 값)임을 알 수 있다.