1. 퍼셉트론(2)

지난 시간 퍼셉트론에 대해서 공부했다.

오늘은 지난 시간 공부한 퍼셉트론과 퍼셉트론의 한계점을 어떻게 극복하는지에 대해 알아보고자 한다.

 

※ 퍼셉트론의 한계

지난번에는 NAND, AND, OR 게이트에 대해서 알아보았다. 이번에는 XOR 게이트에 대해 알아보자.

x1	x2	y
0	0	0
1	0	1
0	1	1
1	1	0

XOR 게이트는 x1과 x2가 같으면 0을, 다르면 1을 출력하는 논리연산이다.

XOR 게이트를 매개변수를 활용하여 출력시키려 해보았을 때, 위치를 좌표에서 나타내어 보자.

O : 0을 출력, ㅁ : 1을 출력

이처럼 1차식이 아닌 비선형의 곡선을 통해서만 구역을 나눌 수 있다.

이것이 바로 단층퍼셉트론의 한계점이다. 단층퍼셉트론은 1차식의 형태를 띄고 있으므로 오로지 선형적으로 표현될 수 있는 게이트에서만 적용이 가능했다.

 

Solution : 이러한 문제점의 해결책은 다층퍼셉트론의 사용이다.

 

 

 

 

 

※ 다층퍼셉트론을 사용한 XOR 게이트 구현

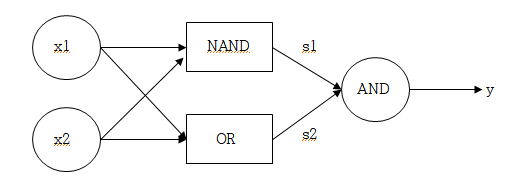
이와 같은 그림으로 형성된다. 여기서 input 과정은 0층, NAND,OR 작업을 한 후 s1, s2가 존재하는 지점을 1층, AND 작업 후 y가 존재하는 output과정을 2층이라고 부른다. 그래서 이 퍼셉트론은 '2층 퍼셉트론'이라고 부른다.

 

import numpy as np

def AND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.7
    temp = np.sum(w*x) + b
    if temp <= 0:
        return 0
    else:
        return 1
    
def NAND(x1, x2):
    x = np.array([x1, x2])
    w = np.array([-0.5, -0.5])
    b = 0.7
    temp = np.sum(w*x) + b
    if temp <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])
    w = np.array([0.5, 0.5])
    b = -0.2
    temp = np.sum(w*x) + b
    if temp <= 0:
        return 0
    else:
        return 1

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

지난 시간의 AND, OR, NAND 게이트 함수를 재귀적으로 사용하여 XOR 함수를 구현할 수 있었다.

 

결과 역시 잘 나오는 것을 확인할 수 있다. 이렇듯 단층퍼셉트론으로 표현하지 못하는 경우에는 층을 하나 늘려 구현을 할 수 있다.