cs231n 3강 - Loss Function & Optimization
※ Loss Function
- Loss Function tells how good our current classifier is!!!
- 모델의 확률 분포와 데이터의 실제 확률 분포 사이의 차이를 나타내는 함수
- loss function 값이 클수록 오차가 크고, loss function 값이 작을수록 오차가 작다.
- loss function 값을 최소화 하는 W, b를 찾아나가자.

loss function은 x를 이미지, y를 정답 label로 사용하여 비교한다.
■ SVM에서의 loss

SVM loss에서는 Sj를 잘못된 label score, Syi를 올바른 label score로 표기하고 계산한다.
첫번째 loss값 = max(0, 5.1 - 3.2 + 1) + max(0, -1.7 - 3.2 + 1) = 2.9
두번째 loss값 = max(0, 1.3 - 4.9 + 1) + max(0, 2.0 - 4.9 + 1) = 0
세번째 loss값 = max(0, 2.2 - (-3.1) + 1) + max(0, 2.5 - (-3.1) + 1) = 12.9
최종 L 값 = (2.9 + 0 + 12.9) / 3 = 5.27
Q1) What happens to loss if car scores change a bit?
A1) 값이 미세하게 바뀐다고 해서 loss 값이 변하지는 않습니다.
Q2) What is the min/max possible loss?
A2) min : 0, max : 무한대
Q3) At initialization W is small so all s ≒ 0. What is the loss?
A2) max(0 - 0 + 1) + max(0 + 0 + 1) = 2
-> Loss 값 = class 개수 - 1
Q4) What if the sum was over all classes?(including j = y_i)
A4) j = y_i의 경우 포함 시 모두 1씩 증가
Q5) What if we used mean instead of sum?
A5) 큰 의미 없음
Q6) What if we used square?
A6) Square를 하게 되었을 때 non-linear 하기 때문에 결과 자체에 차이가 있다.

Q) Loss가 0이라면 Unique 한 Weight 값이 있을까?
A) No. Loss가 0이라도 unique한 Weight 값은 없다. W에 2배를 해도 Loss는 변하지 않는다.
모든 margin이 1보다 크다면 2배, 3배, 4배를 하더라도 Loss는 0으로 고정이다.
지금의 loss는 오직 data의 loss에만 신경을 쓴다. training data에만 신경을 쓰는 Weight를 선택한다면 overfitting을 피할 수 없다.

이 상황을 피하기 위해서 R(W) - Regularization을 더해준다.

이렇게 training data에 집중하는 data loss와 test data에 집중하는 Regularization이 서로 경쟁하면서 최적의 Loss 값을 도출하게 된다.(A way of trading off training loss and generalization loss on test set.)
■ L2 Regularization

더욱 선호되는 방식이다. Weight를 최대한 spread out 해서 Input feature들을 골고루 고려하길 원한다.(diffuse over everything)
■ Softmax Classifier
- scores = unnormalized log probabilities of the classes.
- exp과정과 정규화 과정을 거쳐 최종적인 log스케일의 loss 값을 얻어내는 방식

Softmax Function과 scores 값을 가지고 Log 스케일의 loss 식을 도출해낼 수 있다. 아래의 summary 식을 cross entropy loss라고 부른다. cross entropy loss를 통해서 제대로 된 class에 대한 log 확률을 최대화 하고자 하는 방식 => 정확한 class의 -log 확률을 최소화하고자 하는 방식이다.

ppt에서 제공한 exp과정과 normalize 과정을 거쳐 probabilites를 얻어내고 각각의 log 스케일의 cross entropy loss를 구해내는 방식이다.
Q1) What is the min/max possible loss L_i?
A1) min = 0, max = 무한대 => SVM과 동일하다.
Q2) Usually at initialization W is small so all s ≒ 0. What is the loss?
A2) exp 과정 전 값이 모두 0, exp(0) = 1 이므로 normalize가 끝난 확률은 1/3이다. loss값은 -log(1/3)이다.

지금까지 소개했던 linear classification 과정 이후 SVM의 hinge loss 과정과 Softmax의 cross-entropy loss 과정을 한 눈에 볼 수 있게 ppt에 소개된 내용을 첨부한다.
■ Softmax vs SVM
- Softmax
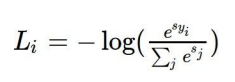
모든 데이터의 변화를 예민하게 관찰하기 때문에 Loss값의 변화가 눈에 띈다.
- SVM

SVM은 둔감하므로 Loss 값이 거의 변하지 않는다.
이제 우리의 고민은 "그렇다면 어떻게 Weight와 bias를 잘 찾아낼 수 있을까?" 이다. 바로 최적화!!!
※ Optimization
1. Random search - very bad idea solution


Accuracy = 15.5%
2. 경사하강법
- 1-dimension : numerical gradient

수치 미분을 이용해서 모든 loss 값을 직접 대입하여 계산하고 증감을 파악할 수 있다.
하지만, 이 방식은 굉장한 시간 소모가 필요하기 때문에 우리는 Analytic gradient 방식을 사용한다. 또한, 단순하게 loss값은 Weight를 구하는 함수라는 것을 잊지 말자!!! 그렇다면 단순하게 Weight 값만 잘 찾으면 된다.
Use calculus to compute an analytic gradient!!!

하지만, 여기서 analytic gradient 방식을 사용할 때 error와 구현이 힘들 수 있다. 그래서 우리는 수치 미분으로 적절하게 잘 구현되었는지 값을 체크해 볼 필요는 있다. 이러한 방식을 gradient check 라고 한다.

ppt에 소개된 SGD의 일반적인 방식이다. mini-batch를 사용하여 적당한 갯수로 줄여서 학습을 시도하고 있다.
또한, step-size를 learning rate로 두었고, 경사하강을 위해서 음수처리를 해 주었다.
여기서 learning rate가 가장 골칫덩어리인 하이퍼파라미터인데 추후에 이 하이퍼파라미터에 대해서 다룬다.

경사하강법을 잘 보여주는 그림이다.