5. 신경망 학습 관련 기술(6)

※ 하이퍼파라미터 최적화

1. 훈련 데이터 : 매개변수의 학습에 이용

2. 검증 데이터 : 하이퍼파라미터 성능 평가에 이용

3. 훈련 데이터 : 신경망의 범용 성능 평가에 이용

 

■ 검증 데이터를 사용하는 이유?

- 시험 데이터를 사용하여 하이퍼파라미터를 조정하게 되면 시험 데이터에 하이퍼파라미터 값이 오버피팅 된다. 시험 데이터에만 적합성을 띄게 되어 범용 성능을 평가하는데 부정확하다. 이로써, 하이퍼파라미터의 성능을 평가하는 검증 데이터가 필요하다.

 

■ 검증 데이터는 무엇인가?

- 일반적으로 데이터셋의 20% 정도를 분리시켜 사용한다.

- 데이터를 분리하기 전에 np.random.shuffle을 사용하여 정답과 입력 데이터를 섞어주고 validation_rate = 0.2로 설정하여 x 형상과 같은 모양의 입력 데이터에 곱해준다.

 

■ 하이퍼파라미터 최적화란?

- 하이퍼파라미터의 최적 값이 존재하는 범위를 조금씩 줄여나간다는 의미

- 대략적인 범위를 설정하고 그 범위에서 무작위로 하이퍼파라미터 값을 샘플링한 후 그 값으로 정확도를 평가한다.

 

0단계 - 하이퍼파라미터 값 범위 설정

1단계 - 설정된 범위에서 무작위로 하이퍼파라미터 값을 샘플링

2단계 - 1단계에서 샘플링 한 파이퍼파라미터 값을 사용하여 학습, 검증 데이터로 정확도를 평가(epoch은 작게 - 시간문제)

3단계 - 1,2 단계 반복, 정확도 결과를 보고 하이퍼파라미터의 범위를 좁힘

 

참고 - 베이지안 최적화: [ML] 베이지안 최적화 (Bayesian Optimization) (tistory.com)

[ML] 베이지안 최적화 (Bayesian Optimization)

 

 

# coding: utf-8
import sys, os
sys.path.append(os.pardir)  # 부모 디렉터리의 파일을 가져올 수 있도록 설정
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist
from common.multi_layer_net import MultiLayerNet
from common.util import shuffle_dataset
from common.trainer import Trainer

(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True)

# 결과를 빠르게 얻기 위해 훈련 데이터를 줄임
x_train = x_train[:500]
t_train = t_train[:500]

# 20%를 검증 데이터로 분할
validation_rate = 0.20
validation_num = int(x_train.shape[0] * validation_rate)
x_train, t_train = shuffle_dataset(x_train, t_train)
x_val = x_train[:validation_num]
t_val = t_train[:validation_num]
x_train = x_train[validation_num:]
t_train = t_train[validation_num:]


def __train(lr, weight_decay, epocs=50):
    network = MultiLayerNet(input_size=784, hidden_size_list=[100, 100, 100, 100, 100, 100],
                            output_size=10, weight_decay_lambda=weight_decay)
    trainer = Trainer(network, x_train, t_train, x_val, t_val,
                      epochs=epocs, mini_batch_size=100,
                      optimizer='sgd', optimizer_param={'lr': lr}, verbose=False)
    trainer.train()

    return trainer.test_acc_list, trainer.train_acc_list


# 하이퍼파라미터 무작위 탐색======================================
optimization_trial = 100
results_val = {}
results_train = {}
for _ in range(optimization_trial):
    # 탐색한 하이퍼파라미터의 범위 지정===============
    weight_decay = 10 ** np.random.uniform(-8, -4)
    lr = 10 ** np.random.uniform(-6, -2)
    # ================================================

    val_acc_list, train_acc_list = __train(lr, weight_decay)
    print("val acc:" + str(val_acc_list[-1]) + " | lr:" + str(lr) + ", weight decay:" + str(weight_decay))
    key = "lr:" + str(lr) + ", weight decay:" + str(weight_decay)
    results_val[key] = val_acc_list
    results_train[key] = train_acc_list

# 그래프 그리기========================================================
print("=========== Hyper-Parameter Optimization Result ===========")
graph_draw_num = 20
col_num = 5
row_num = int(np.ceil(graph_draw_num / col_num))
i = 0

for key, val_acc_list in sorted(results_val.items(), key=lambda x:x[1][-1], reverse=True):
    print("Best-" + str(i+1) + "(val acc:" + str(val_acc_list[-1]) + ") | " + key)

    plt.subplot(row_num, col_num, i+1)
    plt.title("Best-" + str(i+1))
    plt.ylim(0.0, 1.0)
    if i % 5: plt.yticks([])
    plt.xticks([])
    x = np.arange(len(val_acc_list))
    plt.plot(x, val_acc_list)
    plt.plot(x, results_train[key], "--")
    i += 1

    if i >= graph_draw_num:
        break

plt.show()

 

하이퍼파라미터 최적화의 구현이다. 입력데이터의 20%로 검증데이터를 만들어준 후 네트워크를 구성하고 먼저 0단계의 범위 설정을 위해 weight_decay와 learning rate를 np.random.uniform로 구현해주었다. 하이퍼파라미터 100개를 무작위로 탐색하며 lr과 weight_decay를 나열하고, 지정해준 범위 내에서 최종적으로 최적화 결과값을 뽑아낸다. Best-1~20까지의 결과표를 보면

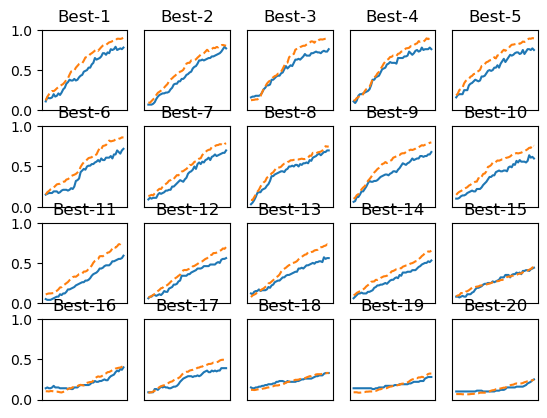
이와 같다. 이를 통해서 Best-1~5 사이에서는 거의 훈련데이터와 검증데이터의 정확도가 유사하고 학습이 잘 진행되는 것을 확인할 수 있다. 그렇다면 이제 Best-1~5에서의 lr과 가중치 값을 살펴보자.

 

Best-1(val acc:0.78) | lr:0.009847428785680918, weight decay:1.6478526249628462e-07
Best-2(val acc:0.77) | lr:0.0071269576582999004, weight decay:4.6278197318541225e-08
Best-3(val acc:0.76) | lr:0.009809153292443666, weight decay:9.896136241849443e-06
Best-4(val acc:0.76) | lr:0.00945848043503819, weight decay:3.4045808596871504e-05
Best-5(val acc:0.75) | lr:0.007279458994402833, weight decay:1.9041530324352e-08

이 lr과 가중치 값을 통해 학습이 잘 진행될 때의 학습률과 가중치 감소 계수의 범위를 다시 좁혀나갈 수 있다. 이렇게 계속 범위를 축소시키면서 작업을 반복하여 특정 단계에서의 최종 하이퍼파라미터 값을 하나 설정하는 것이다.