4. 오차역전파법(2)

이제 계산 그래프 이론으로만 이해했던 오차역전파법을 직접 구현해 볼 차례이다.

 

※ 덧셈 노드 계층

class AddLayer:
    def __init__(self):
        pass

    def forward(self, x, y):
        out = x + y

        return out

    def backward(self, dout):
        dx = dout * 1
        dy = dout * 1

        return dx, dy

AddLayer라는 Class 형태로 덧셈 노드 계층을 구현할 수 있다. 순전파는 그대로를 보내고, 역전파도 그대로 아무것도 하지 않고 출력시키면 되기 때문에 초기화를 pass 시켰고, 순전파와 역전파 역시 우리가 오차역전파법(1)에서 그림으로 보았던 것처럼 그대로 출력을 시켜 주었다.

 

※ 곱셈 노드 계층

class MulLayer:
    def __init__(self):
        self.x = None
        self.y = None

    def forward(self, x, y):
        self.x = x
        self.y = y                
        out = x * y

        return out

    def backward(self, dout):
        dx = dout * self.y  # x와 y를 바꾼다.
        dy = dout * self.x

        return dx, dy

MulLayer라는 Class 형태로 곱셈 노드 계층을 구현할 수 있다. 각자 self를 사용하여 x,y를 구현해주고 순전파는 이를 그대로 곱하는 형태로, 역전파는 x와 y의 입력값을 서로 바꾸어 곱하는 형태로 오차역전파법(1)에서 본 그림을 그대로 코드로 구현했다.

 

 

※ ReLU 계층

앞서 활성화 함수를 배울 때 ReLU 함수의 수식이 어땠는지 기억하는가?

 

ReLU 함수

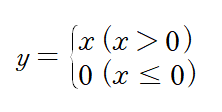
이 함수를 x에 대한 y의 미분을 취해보면

ReLU 함수 미분

 

이러한 형태가 된다는 것을 알 수 있다.

이를 이제 계산 그래프로 나타내어 보자.

 

x > 0

x ≤ 0

 

x가 0 보다 클 경우는 1을 반영한 relu 함수의 미분 값이 그대로 흘러가는 것을 확인할 수 있고, x가 0 이하일 경우에는 0을 반영한 relu 함수의 미분값이 0이 되는 것을 확인할 수 있을 것이다.

 

import numpy as np

class Relu:
    def __init__(self):
        self.mask = None
        
    def forward(self, x):
        self.mask = (x<=0)    # x<=0 일때 True를 반환하게 설정
        out = x.copy()
        out[self.mask] = 0
        
        return out
    
    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        
        return dx

x = np.array([[1.0, -0.5], [-2.0, 3.3]])
print(x)

mask = (x<=0)
print(mask)

mask라는 numpy 배열을 사용하여 x<=0일때 True 값을 반환하도록 해 주었다. 

[[ 1.  -0.5]
 [-2.   3.3]]
[[False  True]
 [ True False]]

결과는 이와 같이 나오게 된다. 여기서 순전파 때의 입력 값이 0 이하일 경우 역전파의 값은 0이 되어야 하므로 역전파 때는 mask numpy 배열의 원소가 True가 되는 지점들은 상류에서 전파된 dout을 0으로 설정해야 한다.

 

 

※ Sigmoid 계층

앞서 배웠던 Sigmoid 함수를 기억하시나요?

sigmoid 함수

 

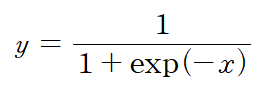
Sigmoid 함수의 계산 그래프를 한 번 나타내어 봅시다.

 

 

복잡한 계산 과정은 "밑바닥부터 시작하는 딥러닝 169p"를 참고하기 바란다.

 

■ 나누기 노드, exp 노드

- / 노드 : y = 1 / x 계산 -> 미분 시 -1/x^2=-y^2을 역전파에 곱해서 흘려보냄

- exp 노드 : y = exp(x) 계산 -> 미분 시 exp(x)를 역전파에 곱해서 흘려보냄

 

 

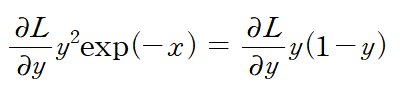
최종적으로 위와 같은 Sigmoid 함수의 역전파 공식이 만들어지게 된다. 이를 잘 기억해 두고 코드로 한 번 구현해 보자.

class Sigmoid:
    def __init__(self):
        self.out = None
        
    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        
        return out
    
    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        
        return dx

 

미분은 dout, y는 self.out으로 구분해서 위 식과 함께 코드를 보게 되면 한 번에 이해할 수 있을 것이다.