AI 모델(딥러닝 기초)/3. 신경망 학습
3. 신경망 학습(3)
Hyeon Lee
2023. 1. 7. 17:44
728x90
※ 수치 미분
일반적으로 우리는 미분 자체를 순간의 변화량으로 판단한다.
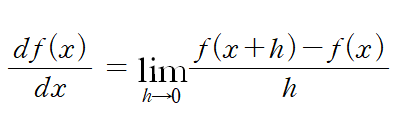
위와 같이 흔히 표현하며 이를 전방 차분이라고 부른다.
하지만, 코드로 위의 식을 구현할 때 몇 가지 고려할 점이 생긴다.
1. lim 표현을 위해 h를 아주 작은 값을 대입하는 방식을 사용하는데, 반올림 오차를 고려하여 이를 e^(-4) 정도로 하는 것이 적당하다.
2. x+h와 x 사이의 함수 f의 차분을 계산하는데, 이 계산에 오차가 존재한다. -> 진정한 미분은 x 위치의 함수의 기울기에 해당하지만 x+h와 x 사이의 차분을 계산하므로 오차가 발생함.
이 두가지 고려사항들을 통해 일반적으로 중심 차분 or 중앙 차분이라고 부르는 방식으로 코드를 구현한다.
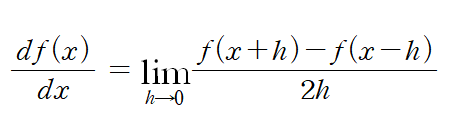
이렇게 표현하는 미분 방식도 눈에 꽤 익숙할 것이다. 중앙 차분으로 코드를 구현해야 오차가 최대한 없는 진정한 미분과 동일한 값이 나오게 된다는 것을 알고 넘어가자.
def numerical_diff(f,x):
h = 1e-4
return (f(x+h) - f(x-h)) / (2*h)
중앙 차분과 반올림 오차를 고려하여 미분을 구현해 주었다.
※ 편미분
- 변수가 여럿인 함수에 대한 미분
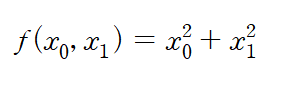
위 함수를 예로 들어보자.
def function(x):
return x[0]**2 + x[1]**2
이 함수를 x0 = 3, x1 = 4 일 때, x0에 대한 편미분을 구하게 되면, 2x0 + x1^2이 된다.
def function_tmp1(x0):
return x0*x0 + 4.0**2.0
이 함수를 x0 = 3, x1 = 4 일 때, x1에 대한 편미분을 구하게 되면, x0^2 + 2x1이 된다.
def function_tmp2(x1):
return 3.0**2.0 + x1*x1
이 함수들을 출력시켜 보자.
print(numerical_diff(function_tmp1, 3.0))
print(numerical_diff(function_tmp2, 4.0))6.00000000000378
8.000000000016882
이렇게 편미분은 변수가 하나인 미분과 마찬가지로 특정 장소의 기울기를 구한다. 여러 변수 중 목표 변수를 지정하고 다른 변수는 값을 고정시켜 계산하면 된다.
728x90